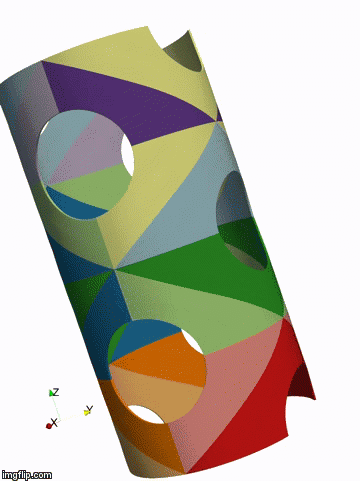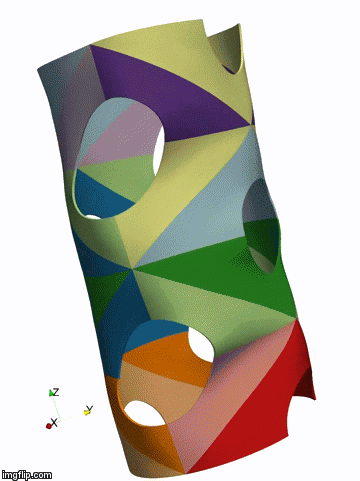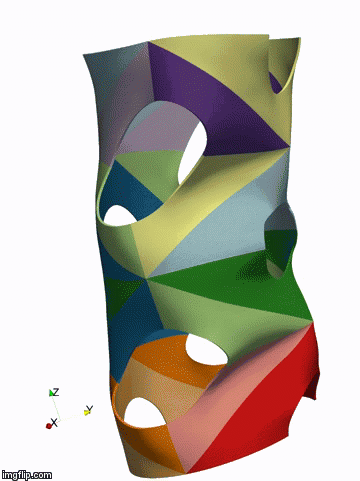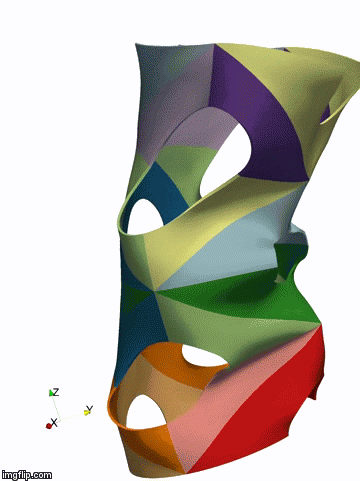Project summary
Models in many areas of scientific and technological
interest (such as solid mechanics, fluid mechanics,
fluid-structure interaction, electromagnetism, ...) are written
in the language of Partial Differential Equations (PDEs). These
equations have rich mathematical structure and their exact
solution is impractical or impossible, for real world
problems. Therefore, so-called numerical methods are studied in
order to approximate the PDE solution by means of a computer
algorithm. The ERC HIgeoM project ("Highly accurate
Isogeometric Method") is aimed at developing one recent and very
promising numerical method, named IsoGeometric Method (IGM). IGM
addresses the interoperability between Computer Aided Design
(CAD) and numerical simulation of PDEs. CAD softwares, used in
industry for geometric modeling, typically describe the geometry
of physical domains by mathematical functions named Non-Uniform
Rational B-Splines (NURBS), and the interface between CAD
output and classical numerical schemes (relying on a different
class of functions) calls for expensive re-meshing methods that
result in approximate representation of domains. IGMs are
NURBS-based schemes for solving PDEs whose benefits go beyond
the improved interaction with CAD. Indeed, they provide a
substantial increase of the accuracy-to-computational-effort
ratio and, thanks to the use of high-degree smooth NURBS within
the numerical scheme, they outperform classical numerical
schemes in most academic benchmarks. However, the mathematical
understanding of the IGM is still incomplete and likely we are
far from exploiting its full potential. The use of higher-degree
IGM for real-world applications asks for new tools allowing for
the efficient construction and solution of the linear system,
time integration, flexible local mesh refinement, and so on. The
HIgeoM research activity is aimed at providing the crucial
knowledge to further develop the IGM into a highly accurate and
stable numerical methodology, having an impact in many fields of
numerical simulation, particularly when accuracy is essential
both in geometry and solution representation. The HIgeoM
project is carried on in Pavia at the Mathematics Department and
in close cooperation with IMATI-CNR (Istituto di Matematica
Applicata e Tecnologie Informatiche E. Magenes, CNR), involving
a large group of PhDs and Post-docs, and spans from very
theoretical research to implementation and testing for complex
applications close to industrial benchmarks.
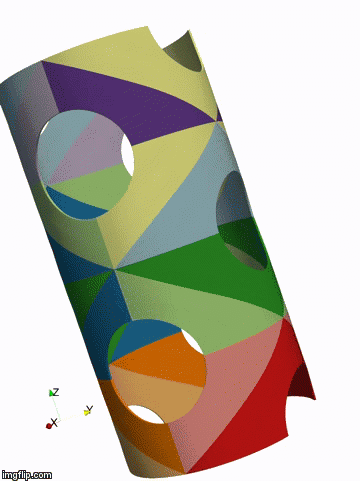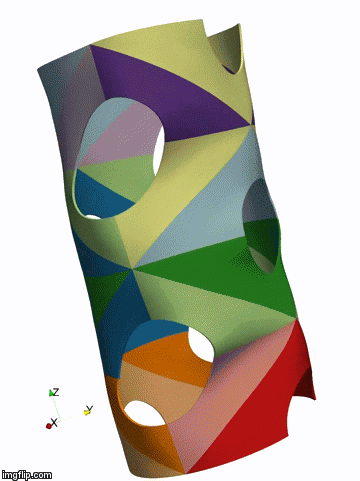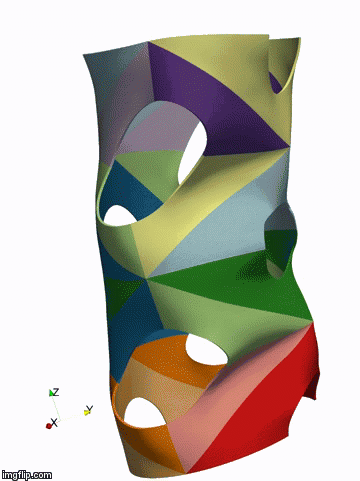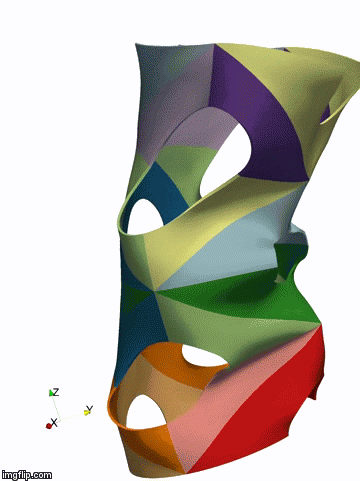
Above: isogeometric simulation of the bukling of a shell represented by 32 NURBS patches (by P. Antolin)
|